Quantitative Analysis of White Matter Fibers
This work is motivated by the premise that the many varied applications of white matter fiber analysis--the differential diagnosis of white matter diseases and neurosurgical planning being two of them--would benefit from the availability of a wider selection of metrics and tools. This would allow us to customize our approach to applications for optimal results.
In my work, I use a new set of methods for the geometrical analysis of fiber tracts. These tools extend the shape analysis of fiber tracts to an analysis of combinations of features. The four physical features--shape, orientation, scale and position-- associated with a fiber modeled as a curve are considered here.
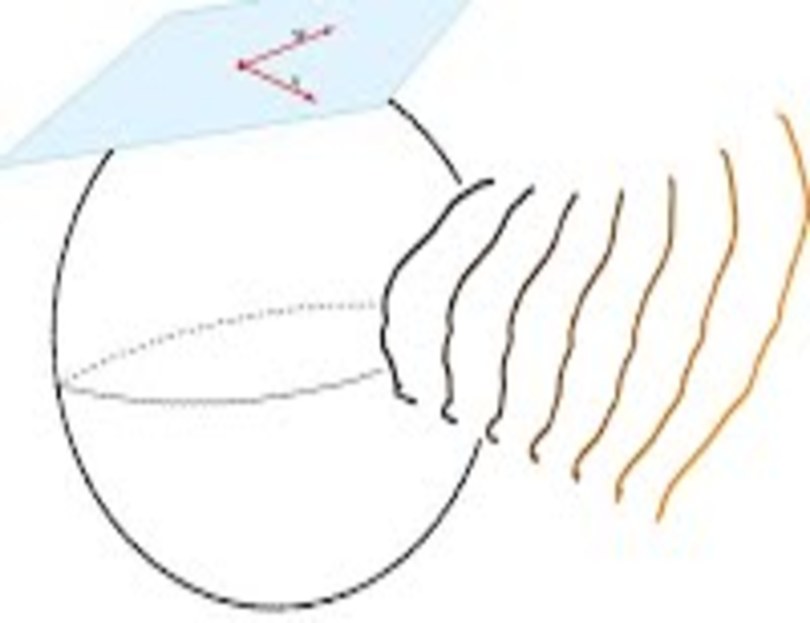
Riemannian framework for the analysis of white matter fiber tracts
A quantitative analysis of white matter fibers is based on physical features such as shape,
scale, orientation and position. Due to the different properties of these features, one usually
designs different metrics and spaces to treat them individually. We propose a comprehensive
Riemannian framework that allows for a joint analysis of these features in a consistent manner.
For each feature combination, we provide a formula for the distance (i.e. a quantification of
differences between two fibers) and a formula for geodesics (i.e. optimal deformations of fibers
into each other).
A description of the methodology can be found in my
PhD thesis, Chapter 3.
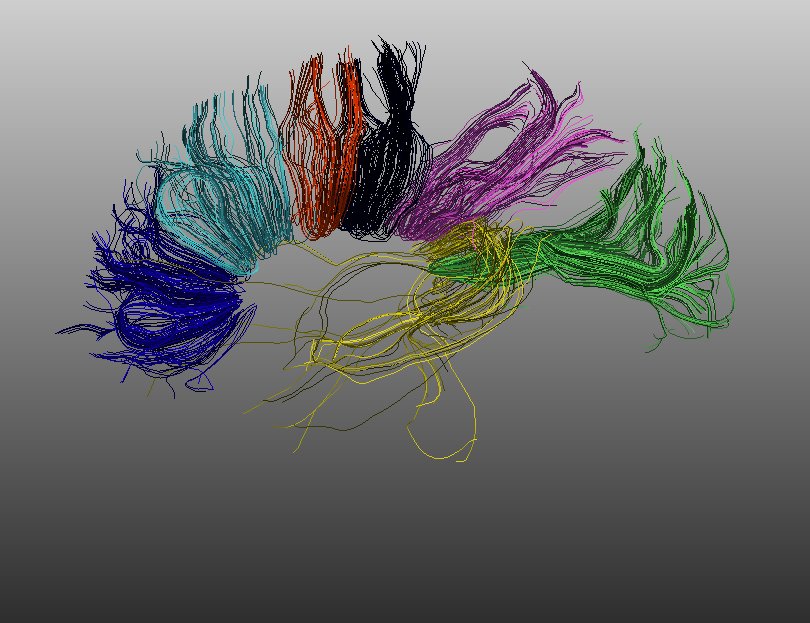
Clustering of corpus callosal fibers
To illustrate this framework we cluster fiber tracts from the corpus callosum and study results
from different combinations of features. We demonstrate how the combined shape+orientation+scale
information gives better discrimination than shape information alone in one case. In another
example we are able to show how the shape+orientation distance gives better results than the
shape+orientation+scale combination of features. Thus we motivate the need for the metrics
defined within the different feature spaces.
Meena Mani, Sebastian Kurtek, Christian Barillot, Anuj Srivastava.
A Comprehensive Riemannian Framework for the
Analysis of White Matter Fiber Tracts, In ISBI, pp. 1101-1104, IEEE, 2010.
DOI: 10.1109/ISBI.2010.5490185
[ Paper ]
[ Slides ]
[ BibTex ]
[ HAL Repository ]
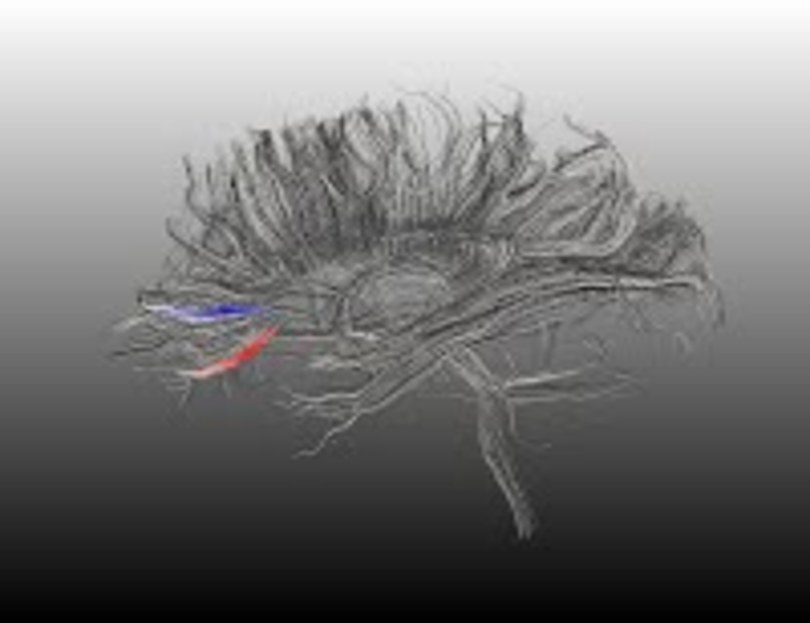
A study of the morphological changes in the corpus callosum
We use metrics (shape and shape+orientation distances) defined within the Riemannian framework
to study morphological changes due to disease progression. We look at sections of the anterior
corpus callosum, which describes a deep arc along the mid-sagittal plane, and show how multiple
sclerosis and normal control populations have different joint shape-orientation signatures. The
broader context of this work is to develop methods to identify and track progressive white
matter disease.
Meena Mani, Anuj Srivastava, Christian Barillot. Morphological changes in the
corpus callosum: A study using joint Riemannian feature spaces, In SPIE Medical
Imaging, pp. 866908-866908,
International Society for Optics and Photonics, 2013.
DOI: 10.1117/12.2007226
[ Paper ]
[ Slides ] [ BibTex ]
[ HAL Repository ]